
Wanneer is iets verjaard? YouTube
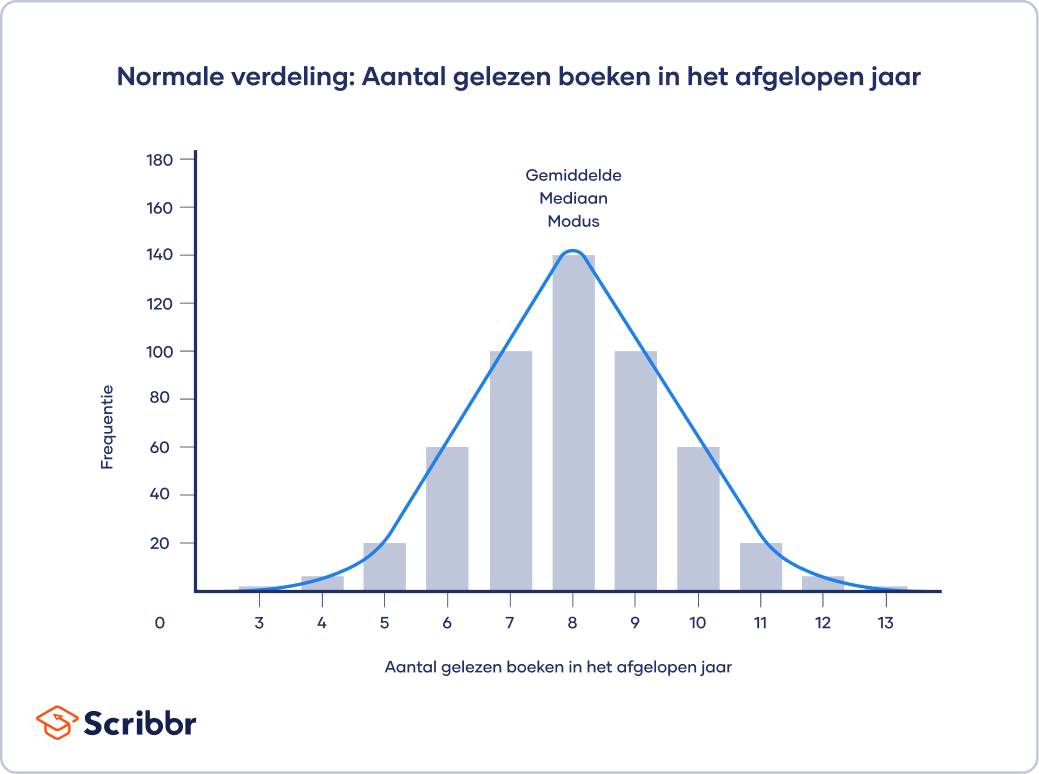
Ongetwijfeld één van de bekendste verdelingen is de normaalverdeling of normale verdeling. De normaal verdeling wordt ook wel de klokcurve en Gauss-kromme genoemd. Bij de normaal verdeling ligt het grootste gedeelte van alle waarden rond het gemiddelde, dit is het hoge deel van de normaal verdeling. Hoe verder je van het gemiddelde verwijdert.
Centrummaten Modus, mediaan en gemiddelde Met voorbeelden
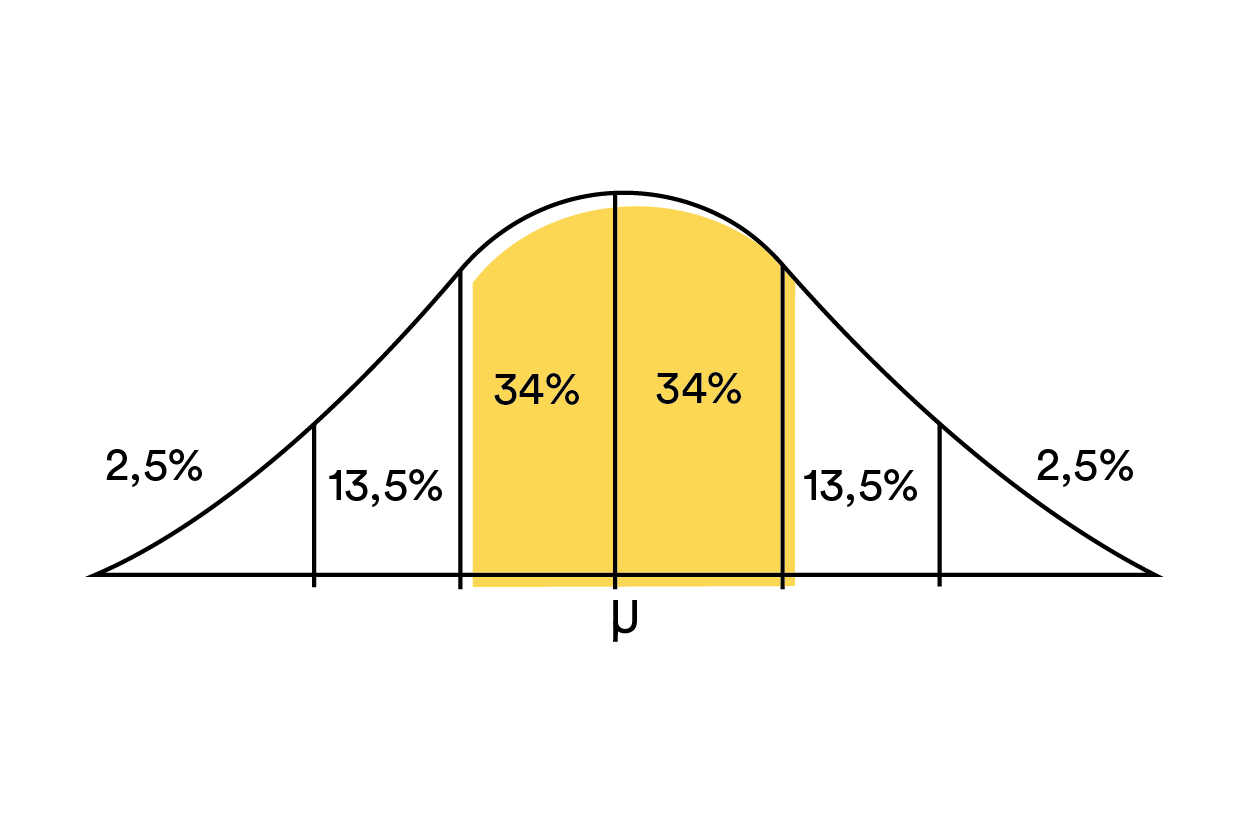
Heeft een symmetrische verdeling een klokvorm zoals hieronder, dan is er sprake van een normale verdeling.. De bijbehorende kromme heet de normaalkromme. Als iets normaal verdeeld is, dan kun je gebruikmaken van de vuistregels van de normale verdeling.
Wat zegt een steekproef? ppt download
Denk eens aan tentamencijfers. Meestal is het zo dat deze normaal verdeeld zijn. Het grootste deel van de mensen scoren rond een 6 of 7, dan zijn er wat mensen die een 8 of 9 halen en een beperkt aantal uitblinkers die tienen scoren. Anderzijds zijn er natuurlijk ook mensen die een 4 of 5 halen en een klein aantal mensen die een 1 of 2 scoren.

mlw stroom 2.1 Statistisch modelleren PDF Gratis download
Veel verschijnselen in de natuur of in de samenleving benaderen de normale verdeling maar zijn niet geheel 'normaal verdeeld'. Te denken valt aan: de verdeling van variabelen als lichaamslengte, gewicht, bloeddruk. Of variaties bij het kruisen van dieren op een bepaalde eigenschap. Bijvoorbeeld schapen met meer of minder wolopbrengst.
Normale verdeling hoe werkt dat en wat kun je ermee? Mr. Chadd
r = rechtergrens. μ = gemiddelde. σ = standaardafwijking. Uitwerking: Antwoord = normalcdf (65, 80, 78, 9) ≈ 0,5136. Dit betekent bij deze normale verdeling dat de kans dat een man een gewicht heeft tussen de 65 kg en 80 kg gelijk is aan 0,5136. Of dat 51,36% van de mannen een gewicht heeft tussen 65 kg en 80 kg. Online normalcdf berekenen.

8.3 Controleren of gegevens normaal verdeeld zijn (lastige opgave) YouTube
Normale verdeling op de grafische rekenmachine. Oppervlakte/kans berekenen met normalcdf. Om een oppervlakte te berekenen onder de normaalkromme gebruik je: TI: normalcdf(l, r, μ, σ) Casio: NormCD(l, r, σ, μ). Hierbij is l de linkergrens, r de rechtergrens, μ het gemiddelde en σ de standaardafwijking. Als er geen linkergrens is, gebruik.

Talent Gewoon ongewoon Ongewoon gewoon Talent is niet normaal. Verdeel ze dus ook niet zo.
Wanneer alle afwijkingen zijn berekend, worden ze allemaal gekwadrateerd en bij elkaar opgeteld. Daarna wordt dit gedeeld door het aantal afwijkingen n.. Alle scores zijn normaal verdeeld met een gemiddeld cijfer van 6,0 en een standaardafwijking van 1,5. De kans dat iemand een 4,5 heeft is dus even groot als de kans dat iemand een 7,5 heeft.

Normaal
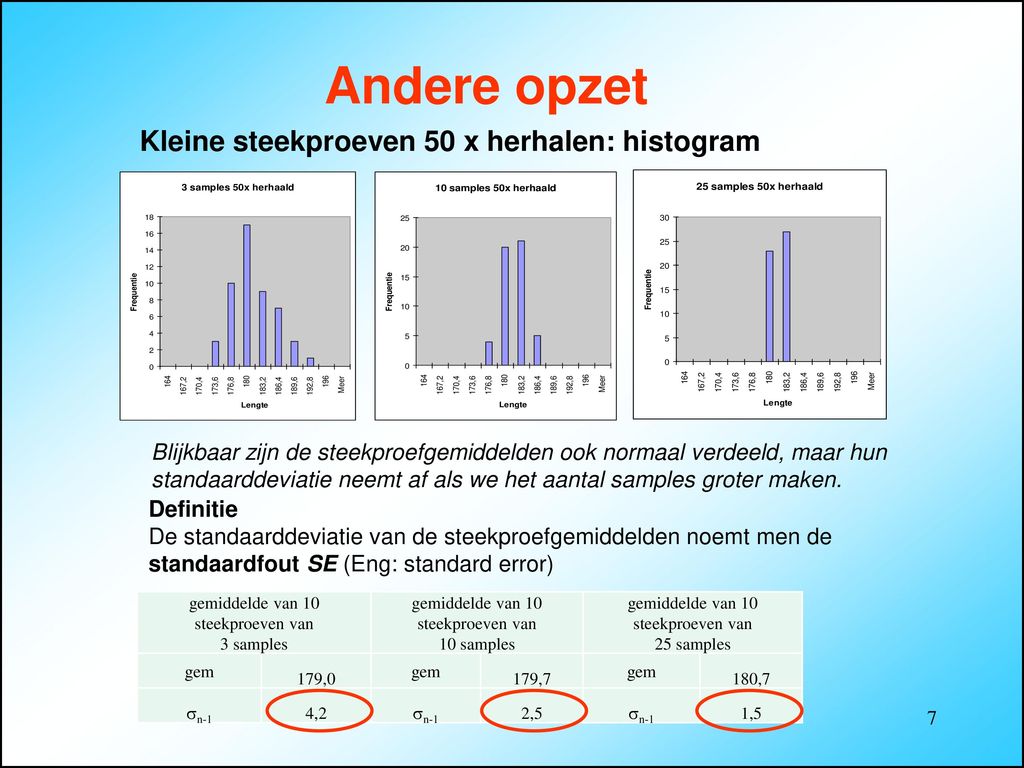
Wanneer is een normale verdeling belangrijk? De aanname van een normale verdeling wordt bij veel statistische toetsen gemaakt. Bij het uitvoeren van een t-toets of anova is de aanname dat de data normaal verdeeld zijn. Bij een regressieanalyse nemen we aan dat fouttermen normaal verdeeld zijn.. De aanname van een normale verdeling is vooral belangrijk bij steekproeven kleiner dan 30 observaties.

voorspellingen
Te bepalen of een variabele normaal verdeeld is. Een normale verdeling heeft zero skew, wat een voorwaarde is voor veel statistische toetsen. Let op Skewness en kurtosis (welving) zijn beide belangrijke maten voor de vorm van een verdeling. Skewness zegt iets over de scheefheid (asymmetrie) van de verdeling, terwijl kurtosis iets zegt over de.
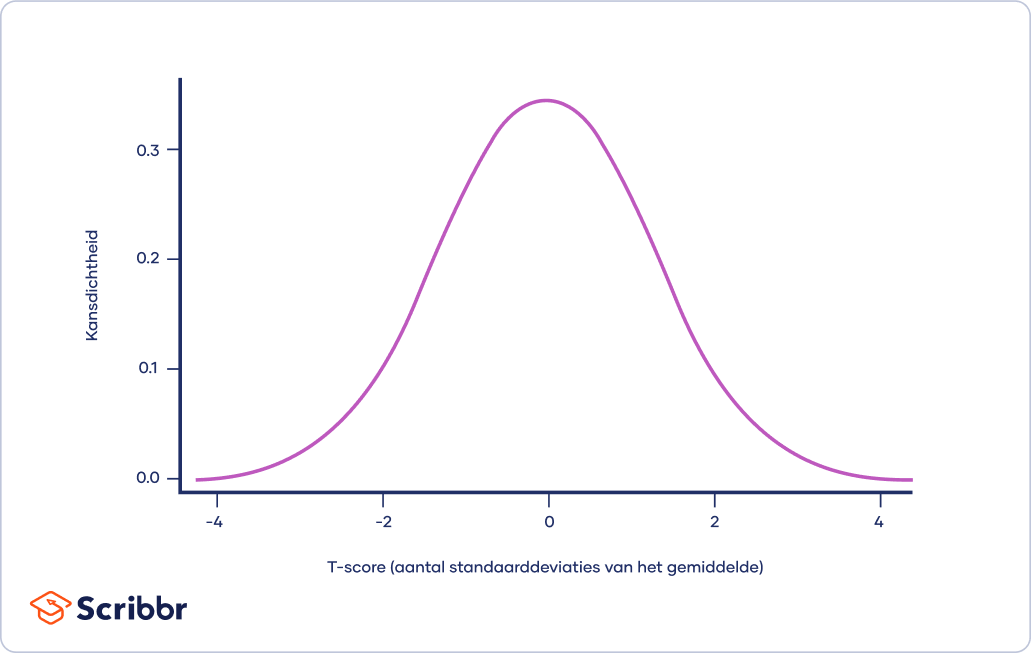
De tverdeling (tdistribution) begrijpen Met voorbeelden
Een normale (of normaal) verdeling is de meest voorkomende continue verdeling. Voorbeelden van normaal verdeelde variabelen zijn lengtes, gewichten, maar ook bijvoorbeeld scores op een test. Een normale verdeling laat zien dat bijvoorbeeld de meeste mensen rond een bepaald gemiddelde scoren. Hoe verder je van het gemiddelde af komt, hoe minder.

Normaalverdeling in excel YouTube
σsteekproevenverdeling = standaardfout = σpopulatie n−−√ σ steekproevenverdeling = standaardfout = σ populatie n. Statistische toetsen hebben als aanname dat de steekproevenverdeling normaal is verdeeld. Je steekproefscores hoeven dus niet normaal verdeeld te zijn. Als je populatieverdeling normaal is verdeeld, is de.
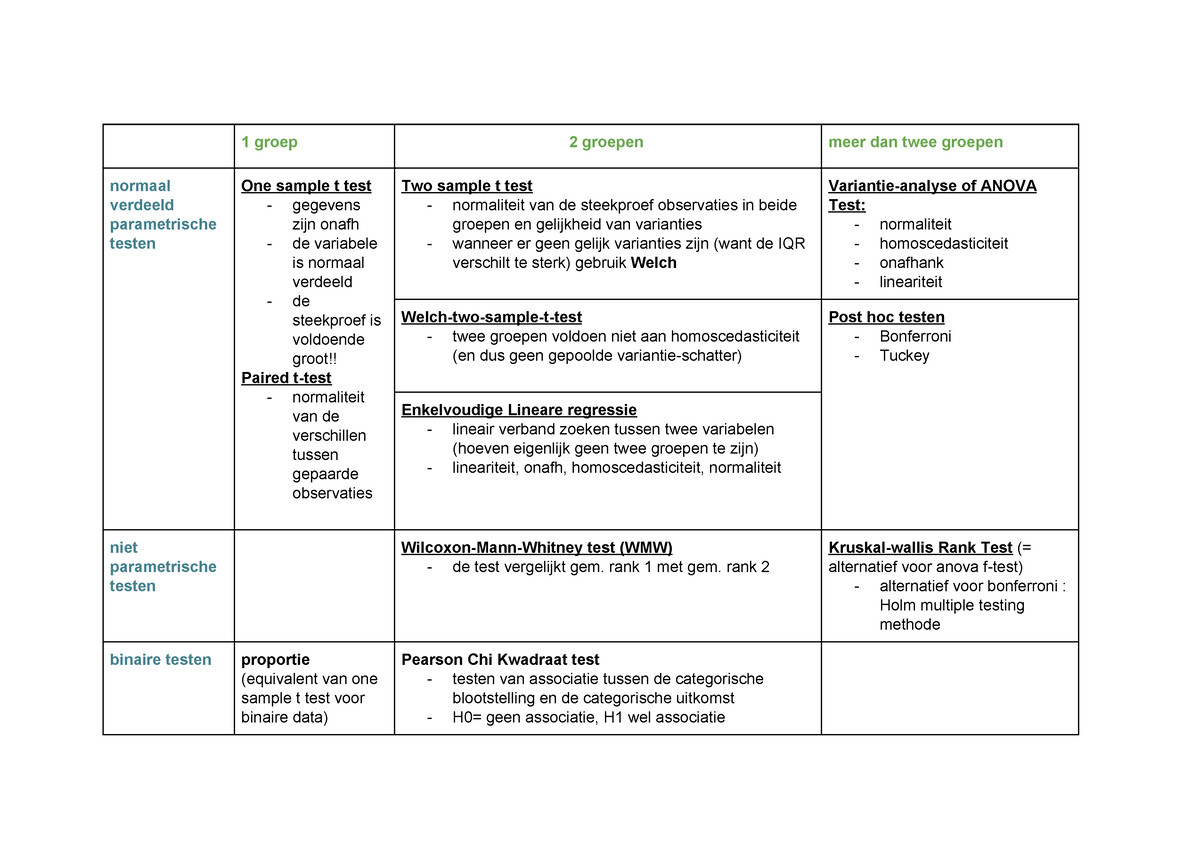
Statistiek testen (tabel) 1 groep 2 groepen meer dan twee groepen normaal verdeeld
Als de variabele normaal verdeeld is, kun je op grond van de z-score zeggen hoeveel procent van de waarnemingen hoger of lager is. Hiervoor. Onderaan staat de maat voor scheefheid (skewness) met de standaardfout. Wanneer de skewness-score minstens twee keer zo groot is als de standaardfout die erachter vermeld wordt, mogen we er niet van.

Normale verdeling Eigenschappen Wiskunjeleren (oud) YouTube
Als je data scheef verdeeld zijn, kan het voorkomen dat je resultaten niet valide zijn. De aanname van een normale verdeling is vooral belangrijk bij steekproeven kleiner dan 30 observaties. Als je steekproef meer dan 30 observaties bevat, dan kun je volgens de centrale limietstelling ( central limit theorem) aannemen dat aan de aanname van.

Waarom is een stabiele bloedsuikerspiegel belangrijk als je wilt afvallen?
Mr. Chadd legt je uit wat je hier precies mee kunt. Een normale verdeling ziet er zo uit als op het plaatje hieronder. Het gemiddelde wordt in een normale verdeling vaak aangegeven met de letter μ (spreek uit als 'mu'). De totale oppervlakte onder de kromme stelt alle getallen voor die in de populatie voorkomen. Dit is dus 100%.
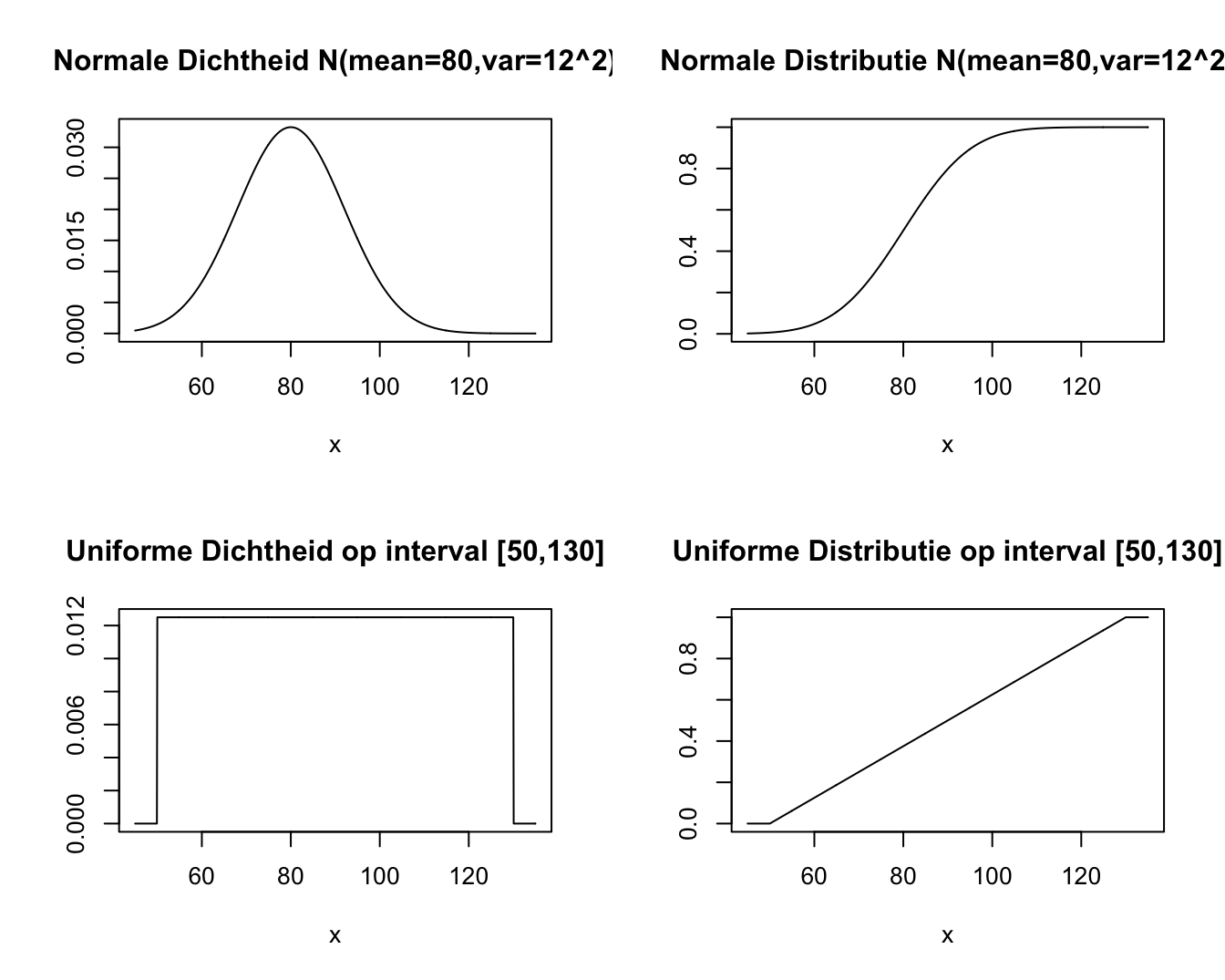
Hoofdstuk 4 Data exploratie en beschrijvende statistiek Cursus Statistiek 20192020
Bijgewerkt op 25 juli 2019. Een normale verdeling van gegevens is er een waarin de meeste gegevenspunten relatief vergelijkbaar zijn, wat betekent dat ze zich voordoen binnen een klein bereik van waarden met minder uitbijters aan de hoge en lage uiteinden van het gegevensbereik. Wanneer gegevens normaal verdeeld zijn, resulteert het plotten.
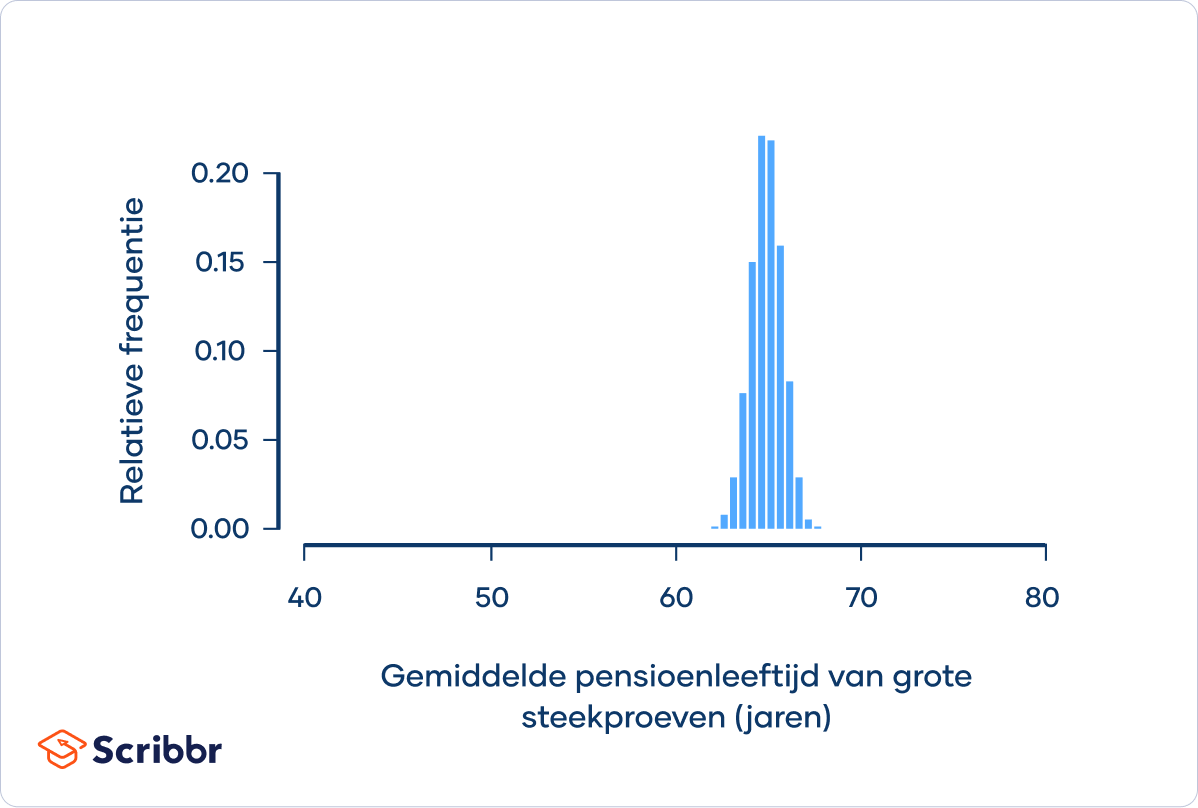
Centrale Limietstelling (Central Limit Theorem) Formule
Meetfouten blijken altijd normaal verdeeld, zo ontdekt Gauss. De gemiddelde meting is goed, maar soms meet je iets te veel en soms iets te weinig. Het is de Belgische wetenschapper Adolphe Quetelet die de normale verdeling voor het eerst op de mens loslaat. Aan het begin van de 19e eeuw legt hij de maten van talloze dienstplichtigen vast.