Linear differential equations second order with variable coefficients Exercise 10B Lalji Prasad


Second Order Non Homogeneous Linear Differential Equations with ics Q10 YouTube

Example 2. Find the general solution of the non-homogeneous differential equation, y ′ ′ ′ + 6 y ′ ′ + 12 y ′ + 8 y = 4 x. Solution. Our right-hand side this time is g ( x) = 4 x, so we can use the first method: undetermined coefficients.


Nonhomogeneous Second Order Differential Equations YouTube

3.3 Nonhomogeneous Linear Second-order Differential Equations A. General Solution of Nonhomogeneous Equations. In this section, we explore the nonhomogeneous linear second-order differential equation of the form:


2nd Order Linear Differential Equations Particular Solutions ExamSolutions YouTube

https://engineers.academy/level-5-higher-national-diploma-courses/In this video, we expand on the principles covered in our introduction to second order diff.


Nonhomogeneous 2ndorder differential equations YouTube

7.1 Second-Order Linear Equations; 7.2 Nonhomogeneous Linear Equations; 7.3 Applications; 7.4 Series Solutions of Differential Equations;. functions, sines, and cosines. So when r (x) r (x) has one of these forms, it is possible that the solution to the nonhomogeneous differential equation might take that same form. Let's look at some.


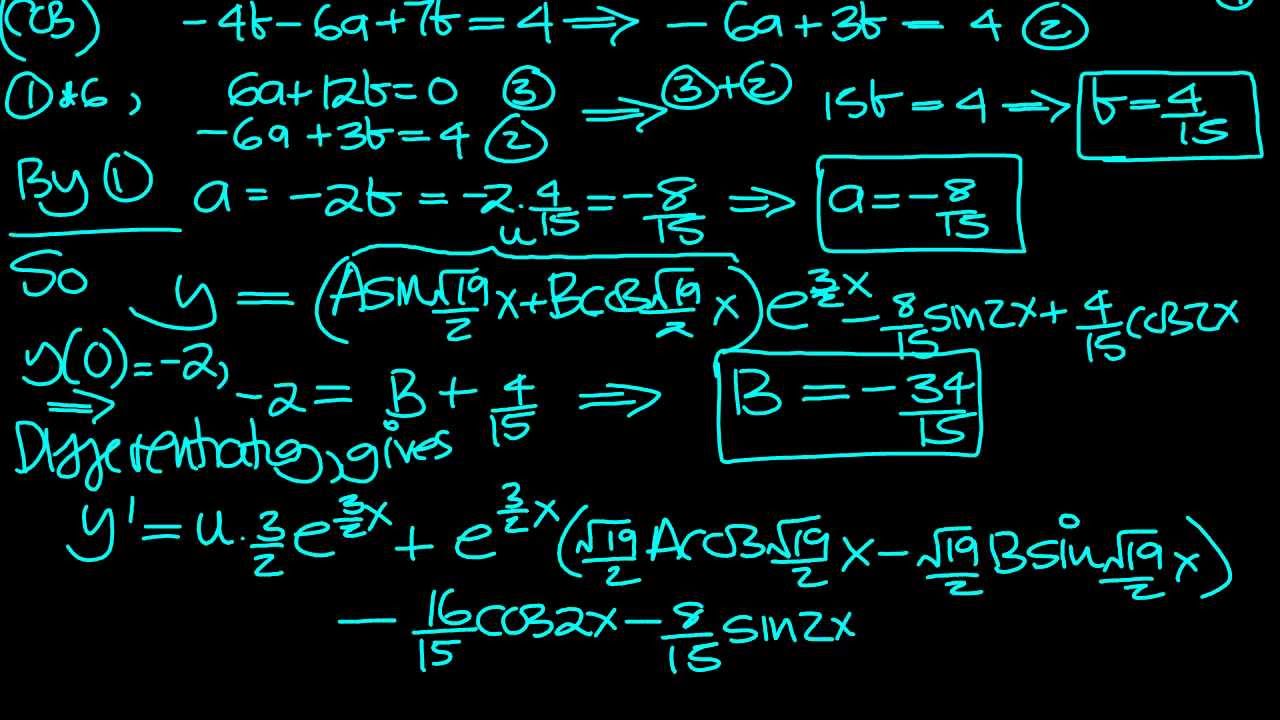
Second Order Non Homogeneous Linear Differential Equations with ics Q2 YouTube

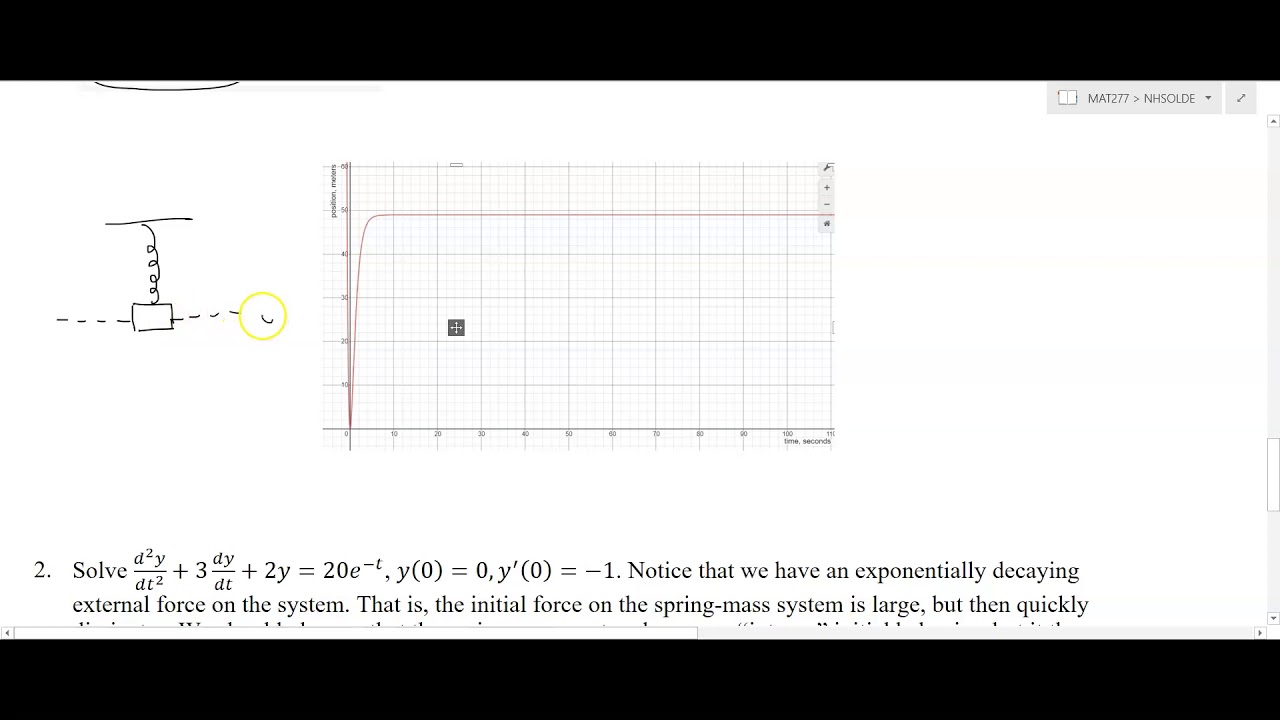
Second Order Nonhomogeneous Linear Differential Equations with Constant Coefficients: a2y ′′(t) +a1y′(t) +a0y(t) = f(t), where a2 6= 0 ,a1,a0 are constants, and f(t) is a given function (called the nonhomogeneous term). General solution structure: y(t) = y p(t) +y c(t) where y p(t) is a particular solution of the nonhomog equation, and y


(PDF) Second Order Linear Nonhomogeneous Differential Equations; Method of Undetermined

It's now time to start thinking about how to solve nonhomogeneous differential equations. A second order, linear nonhomogeneous differential equation is. y′′ +p(t)y′ +q(t)y = g(t) (1) (1) y ″ + p ( t) y ′ + q ( t) y = g ( t) where g(t) g ( t) is a non-zero function. Note that we didn't go with constant coefficients here because.


Particular Solution of NonHomogeneous Differential Equations

This Calculus 3 video tutorial provides a basic introduction into the method of undetermined coefficients which can be used to solve nonhomogeneous second or.


Second order nonhomogeneous differential equation YouTube

second order differential equation: y" p(x)y' q(x)y 0 2. Find the particular solution y p of the non -homogeneous equation, using one of the methods below. 3. The general solution of the non-homogeneous equation is: y(x) C 1 y(x) C 2 y(x) y p where C 1 and C 2 are arbitrary constants. METHODS FOR FINDING THE PARTICULAR SOLUTION (y p) OF A NON.


Chapter 8 Solving Second order differential equations numerically

The formal definition is: f (x) is homogeneous if f (x.t) = t^k . f (x), where k is a real number. It means that a function is homogeneous if, by changing its variable, it results in a new function proportional to the original. By this definition, f (x) = 0 and f (x) = constant are homogeneous, though not the only ones.


Nonhomogeneous Second Order Differential Equations Exam Question [Year 2 Further (Pure Core

Undetermined coefficients is a method you can use to find the general solution to a second-order (or higher-order) nonhomogeneous differential equation. Remember that homogenous differential equations have a 0 on the right side, where nonhomogeneous differential equations have a non-zero function on the right side.


DIFFERENTIAL EQUATIONS 2nd Order NonHomogenous Equation Linear Function Particular Solution

Example 2. Find the general solution of the equation. Solution. We will use the method of undetermined coefficients. The right side of the given equation is a linear function Therefore, we will look for a particular solution in the form. Then the derivatives are. Substituting this in the differential equation gives: The last equation must be.


Second Order Nonhomogeneous Cauchy Euler Differential Equations YouTube

Lecture 22 : NonHomogeneous Linear Equations (Section 17.2) NonHomogeneous Second Order Linear Equations (Section 17.2) Example. The solution of a second order nonhomogeneous linear di erential equation of the form. ay00 + by0 + cy = G(x) where a; b; c are constants, a 6= 0 and G(x) is a continuous function of x on a given interval is of the form.


Particular Solution of a Nonhomogeneous Linear SecondOrder Differential Equation with Constant

In this section we will work quick examples illustrating the use of undetermined coefficients and variation of parameters to solve nonhomogeneous systems of differential equations. The method of undetermined coefficients will work pretty much as it does for nth order differential equations, while variation of parameters will need some extra derivation work to get a formula/process we can use.


Variation of parameters Solving Nonhomogeneous Second Order Differential Equations Part 5

Solving a non-homogeneous differential equation using the Laplace Transform.. page 128, initial conditions for a second-order differential equation are of the form y(t_0) = y_0; y'(t_0) = y'_0, where t_0 may be nonzero.. so you're probably more warmed up than I am. So if we have the equation the second derivative of y plus y is equal to.


Second order non homogeneous differential equation YouTube

17.2: Nonhomogeneous Linear Equations. Now we consider second order equations of the form ay¨ + by˙ + cy = f(t), with a, b, and c constant. Of course, if a = 0 this is really a first order equation, so we assume a ≠ 0. Also, much as in exercise 20 of section 17.5, if c = 0 we can solve the related first order equation ah˙ + bh = f(t), and.


Solving NonHomogenous Second Order Differential Equations YouTube

How to solve a second-order nonhomogeneous linear differential equation with constant coefficients? The example of a mass at the end of a vibrating string is used taking into account spring force, damping force and an external force. Math-Explained by TU Delft OpenCourseWare is licensed under a Creative Commons Attribution-NonCommercial.