
How To Find Moment Of Inertia Of A Rectangular Beam TOKHOW
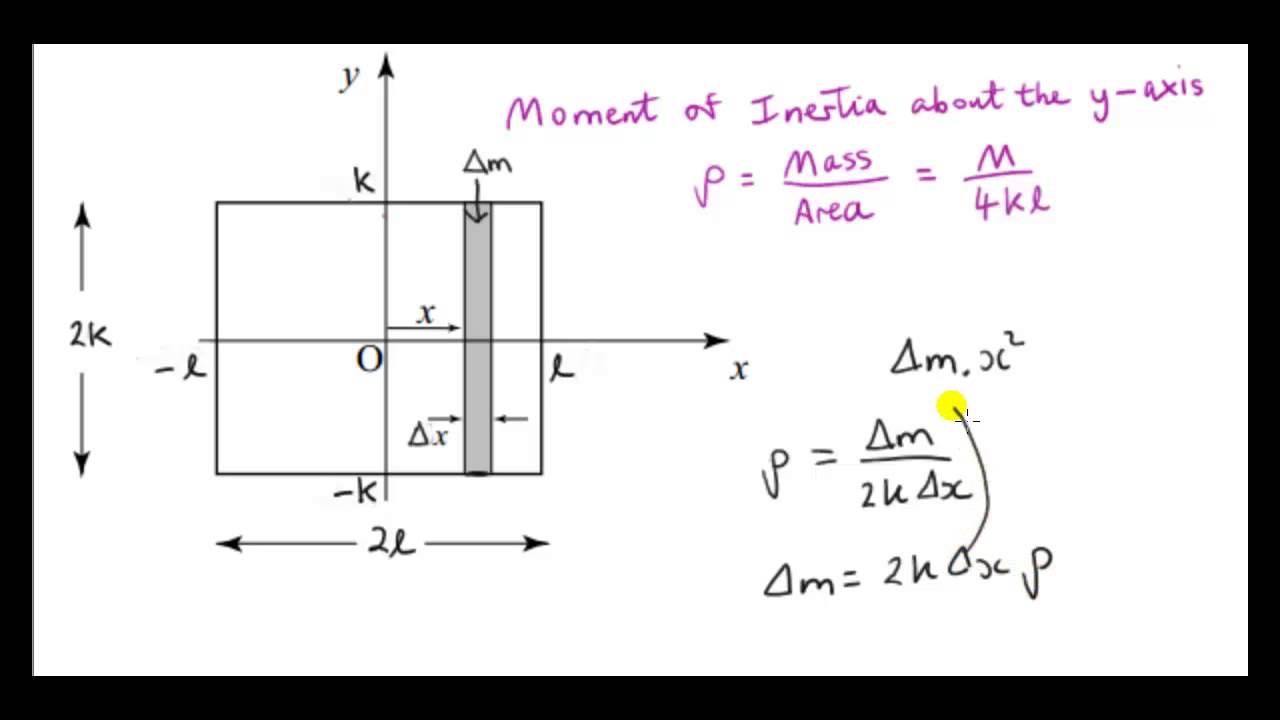
Next, we calculate the moment of inertia for the same uniform thin rod but with a different axis choice so we can compare the results. We would expect the moment of inertia to be smaller about an axis through the center of mass than the endpoint axis, just as it was for the barbell example at the start of this section.

Beam Deflection Moment Of Inertia Images and Photos finder
The moment of inertia can be derived as getting the moment of inertia of the parts and applying the transfer formula: I = I 0 + Ad 2. We have a comprehensive article explaining the approach to solving the moment of inertia. Fundamentally, the moment of inertia is the second moment of area, which can be expressed as the following:

Moment Of Inertia Formula For Rectangular Beam slideshare
The polar moment of inertia J0 for a thin-walled ring can be derived by considering a small area dA of the ring (see figure 3): Figure 3 With: 2 2 2 2 3 3 0 2 2 2 2 2 A J r dA R dA R t d R t π π π π θ π + + − − = = = =∫ ∫ ∫ (10) And finally, for the area moment of inertia with respect to the (principal) x- and y- axis, Ix and Iy.
Moment Of Inertia Thin Walled Rectangular Beam The Best Picture Of Beam
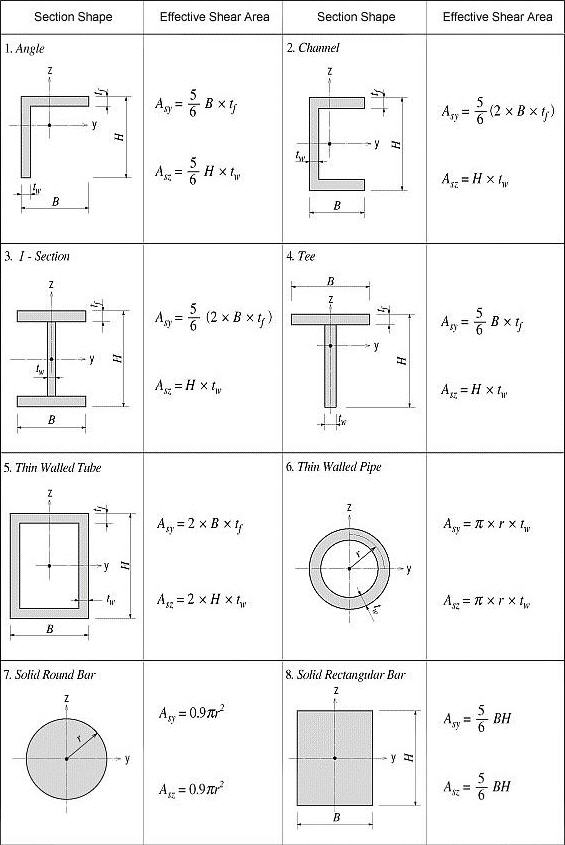
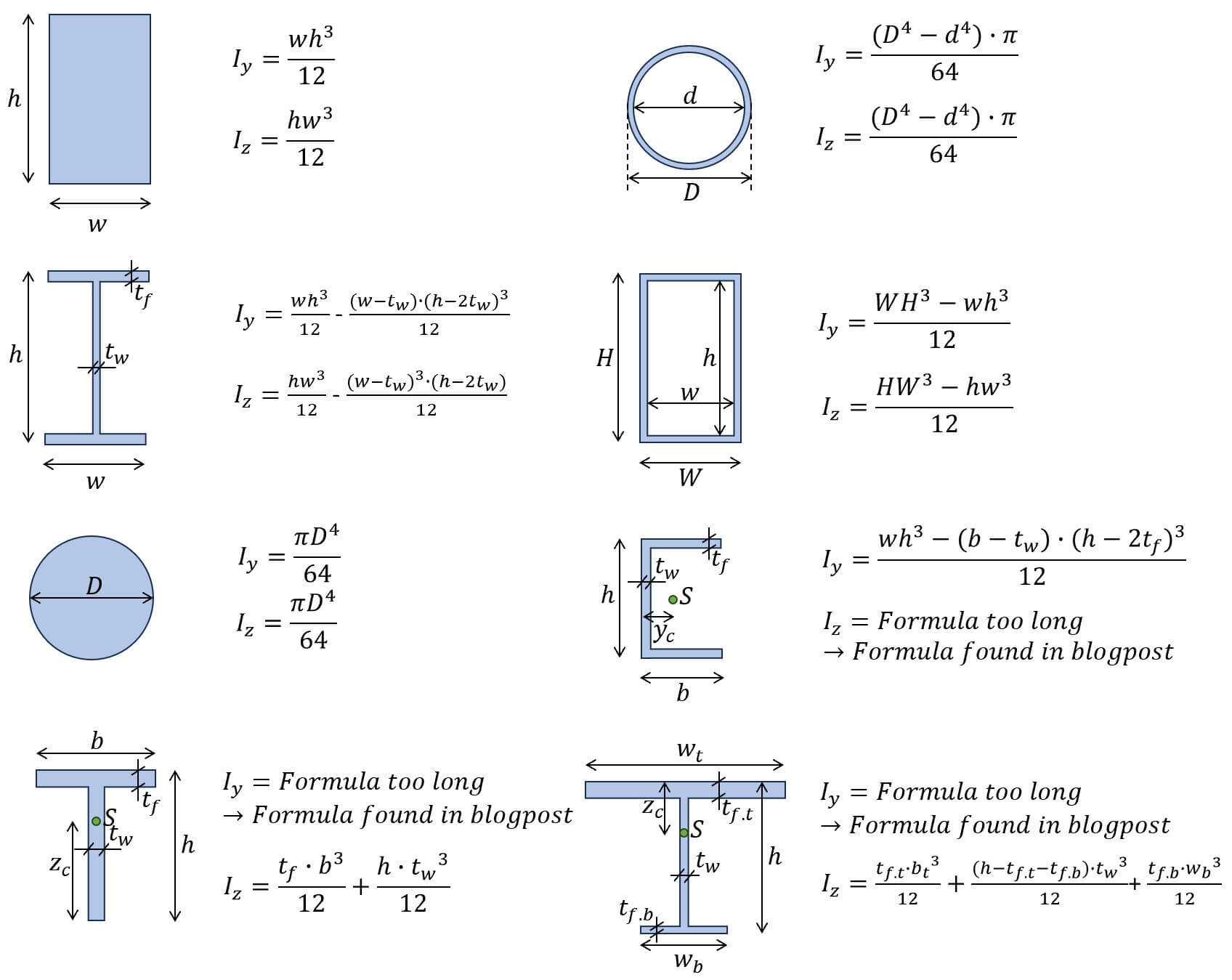
Overview of moment of inertia formulas for different cross-sections. 1. Moment of inertia - Rectangular shape/section (formula) 2. Moment of inertia - I/H shape/section (formula) 3. Moment of inertia - Circular shape/section (formula) 4. Moment of inertia - Hollow circular tube Section (formula)

Moment Of Inertia For Rectangular Beam The Best Picture Of Beam
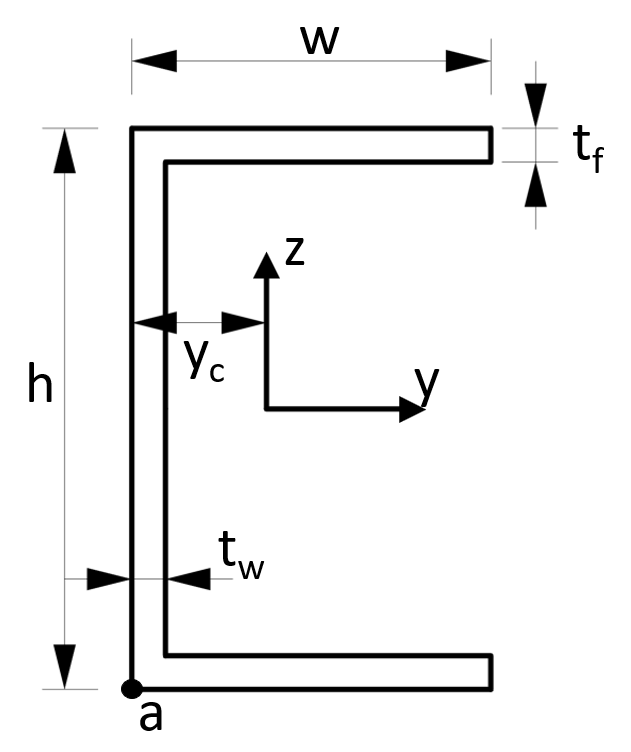
The monosymmetry constant, βX, is used in calculating the buckling moment resistance of laterally unsupported monosymmetric beams loaded in the plane of symmetry (CSA 2000). In the case of a monosymmetric section that is symmetric about the vertical axis, the general formula is given by SSRC (1998): β = 1 ∫ y x. 2. y.

Moment Of Inertia For Beam Deflection New Images Beam
Moment of inertia, denoted by I, measures the extent to which an object resists rotational acceleration about a particular axis, it is the rotational analogue to mass (which determines an object's resistance to linear acceleration).The moments of inertia of a mass have units of dimension ML 2 ([mass] × [length] 2).It should not be confused with the second moment of area, which has units of.
Moment Of Inertia Of Rectangular Section
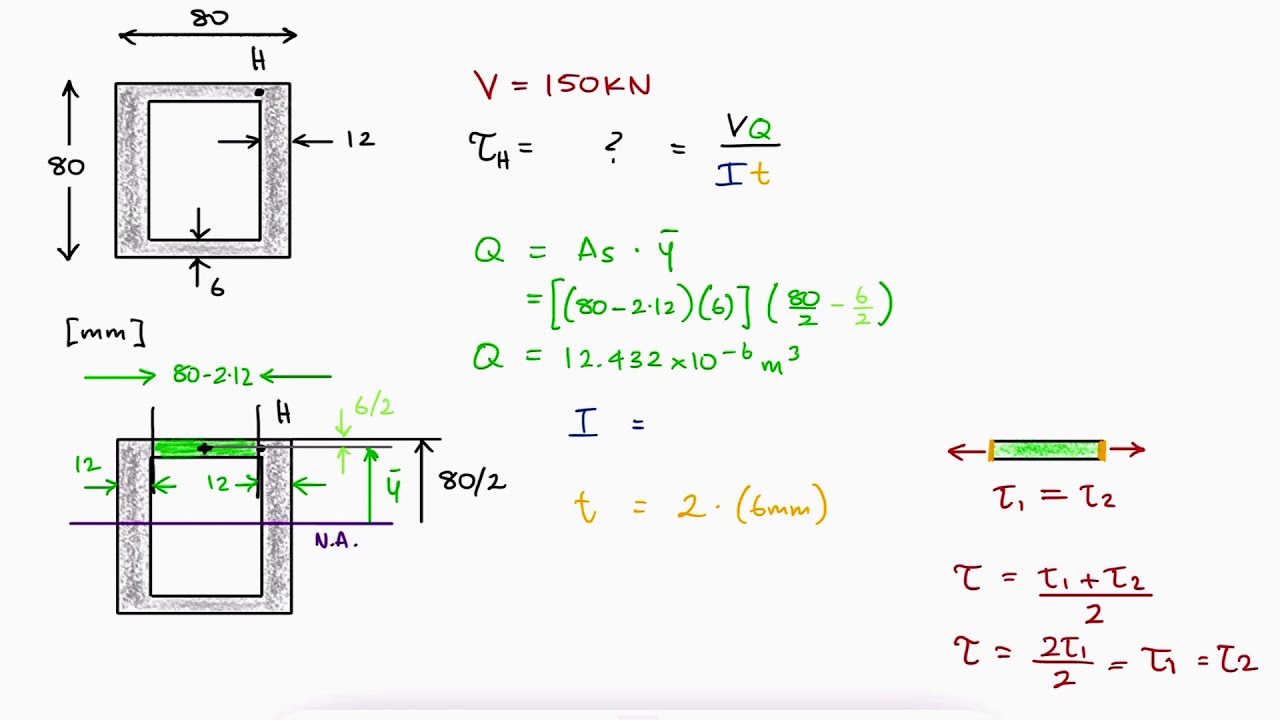
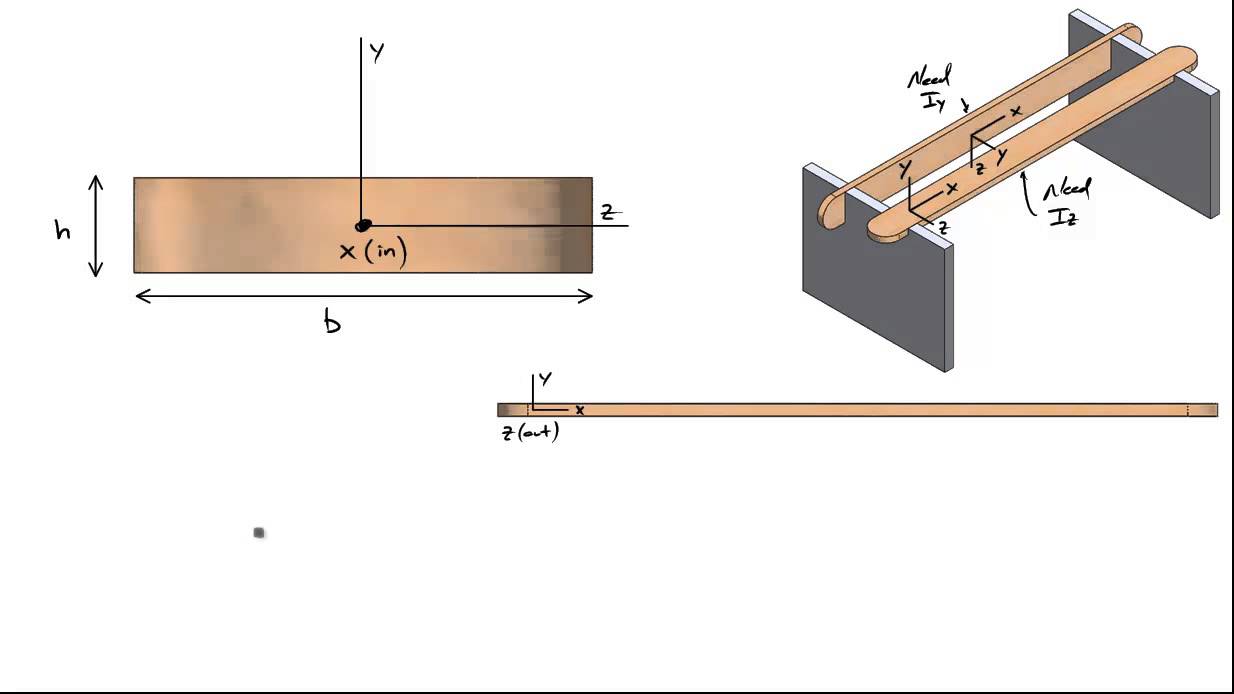
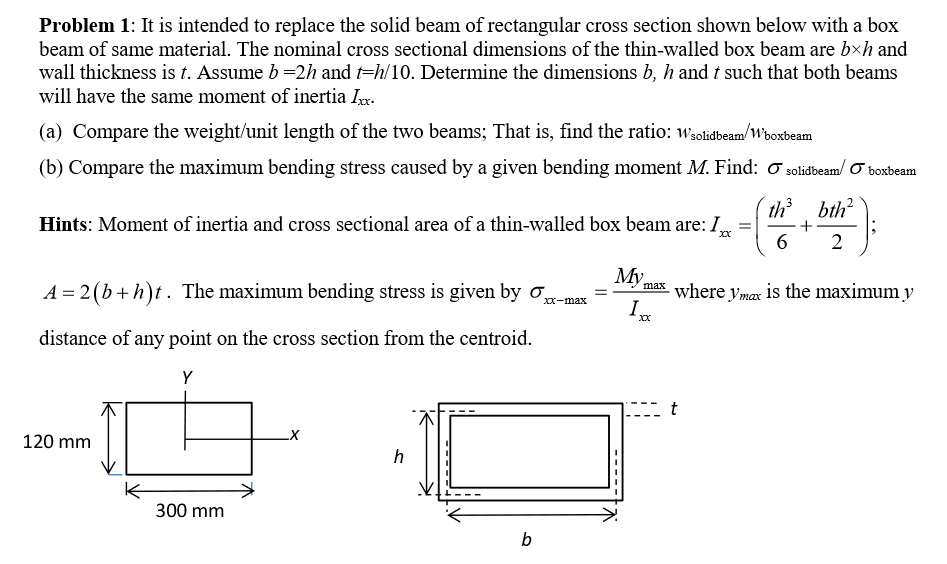
Calculate the second moment of inertia of the beam cross section for: a) Solid rectangular cross section of width b and height h. b) Thin-walled square box section of width and height b. c) Solid circular cross section of radius r. Problem 5-2 Solution: (a) Solid rectangular cross section of width b and height h.
Moment of inertia equation for rectangle genebasta
In summary, the formula for determining the moment of inertia of a rectangle is Ixx=BD³ ⁄ 12, Iyy=B³D ⁄ 12. For rectangular hollow sections, the formula is Ixx=BD³ ⁄ 12 - bd³ ⁄ 12. The moment inertia is important for both bending moment force/stress and deflection. This is evident in their formulas, as in both cases, I (Moment of.
ThinWalled Member BOX BEAM in 3 Minutes! YouTube
Figure 10.6.3: Calculation of the moment of inertia I for a uniform thin rod about an axis through the center of the rod. We define dm to be a small element of mass making up the rod. The moment of inertia integral is an integral over the mass distribution. However, we know how to integrate over space, not over mass.
Moment of Inertia for a Rectangular Beam YouTube
Open section beams • First (static) moment of inertia approach • Function approach iii. Closed section beams b.Torsion of beams i. Free torsion ii. Constrained torsion 3. 4. Plates and shells (2D structures). Shear of open thin-walled beams Arbitrary load split into bending/shear PLUS torsion No torsion = Shear center. 41 Shear of open.

Moment Of Inertia A Hollow Rectangular Beam The Best Picture Of Beam
K = equivalent polar moment of inertia [m 4] For a solid rectangular section, the value of the equivalent polar moment of inertia is: For a thin-walled hollow rectangular section with smooth corners: Example Problem. Problem: A rectangular beam with a width of 200 mm and a height of 100 mm is subjected to a torque of 50 Nm. Determine the.

Moment Of Inertia Basic Shapes
Moments of Inertia for a thin-walled hollow cylinder is comparable with the point mass (1) and can be expressed as:. Moments of Inertia for a rectangular plane with axis along edge can be expressed as. I = 1/3 m a 2. Convert between Area Moment of Inertia units. Cantilever Beams - Moments and Deflections Maximum reaction forces.
Moment Of Inertia Thin Walled Rectangular Beam New Images Beam
Hollow Cylinder . A hollow cylinder with rotating on an axis that goes through the center of the cylinder, with mass M, internal radius R 1, and external radius R 2, has a moment of inertia determined by the formula: . I = (1/2)M(R 1 2 + R 2 2) Note: If you took this formula and set R 1 = R 2 = R (or, more appropriately, took the mathematical limit as R 1 and R 2 approach a common radius R.

Moment of Inertia of Rectangular section M.I of Rectangular section in Strength of Material
Rectangular f max = ⋅ = M c I M Z The section modulus, Z , can be found in many tables of properties of common cross sections (i.e., I-beams, channels, angle iron, etc.). Bending Stress Equation Based on Known Radius of Curvature of Bend, ρ. The beam is assumed to be initially straight. The applied moment, M , causes the beam to assume a.
Moment Of Inertia Formulas For Different Shapes Structural Basics
This free multi-purpose calculator is taken from our full suite Structural Analysis Software. It allows you to: Calculate the Moment of Inertia (I) of a beam section (Second Moment of Area) Centroid Calculator used to calculate the Centroid (C) in the X and Y axis of a beam section. Calculate the First moment of area (Statical Moment of Inertia.

Moment Of Inertia Formula Beam
The moment of inertia of a rectangle with respect to an axis passing through its base, is given by the following expression:. The moment of inertia (second moment or area) is used in beam theory to describe the rigidity of a beam against flexure (see beam bending theory). The bending moment M applied to a cross-section is related with its.