Biot savart law ferdesigners


Biot savart law lasopaairport

Biot-Savart Law. The Biot-Savart Law relates magnetic fields to the currents which are their sources. In a similar manner, Coulomb's law relates electric fields to the point charges which are their sources. Finding the magnetic field resulting from a current distribution involves the vector product, and is inherently a calculus problem when the distance from the current to the field point is.


Applications of Biot Savart Law Class 12 YouTube

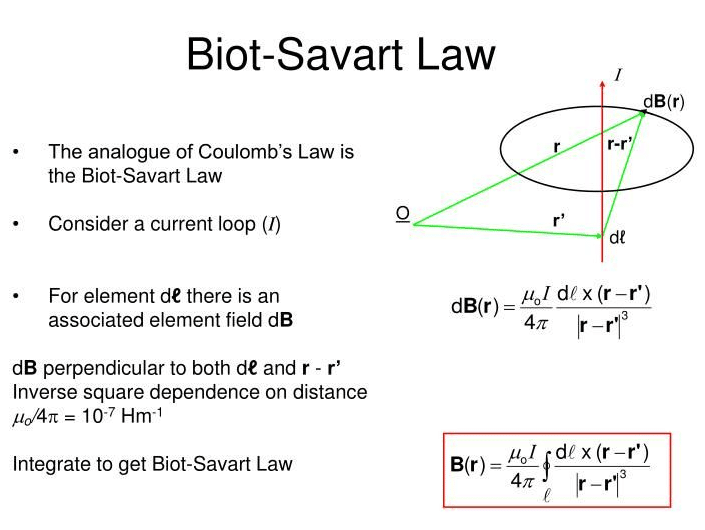
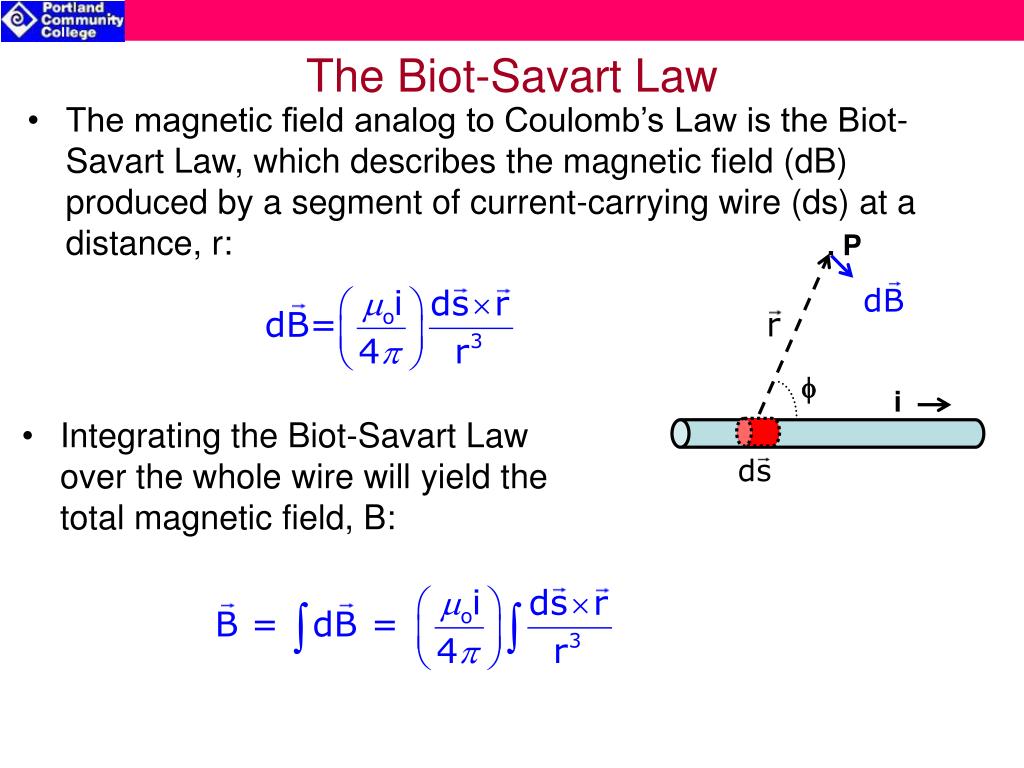
The Biot-Savart law states that at any point P (Figure 12.2.1 ), the magnetic field d→B due to an element d→l of a current-carrying wire is given by. d→B = μ0 4π Id→l × ˆr r2. The constant μ0 is known as the permeability of free space and is exactly. μ0 = 4π × 10 − 7T ⋅ m / A. in the SI system.


Biot savart law britishwes

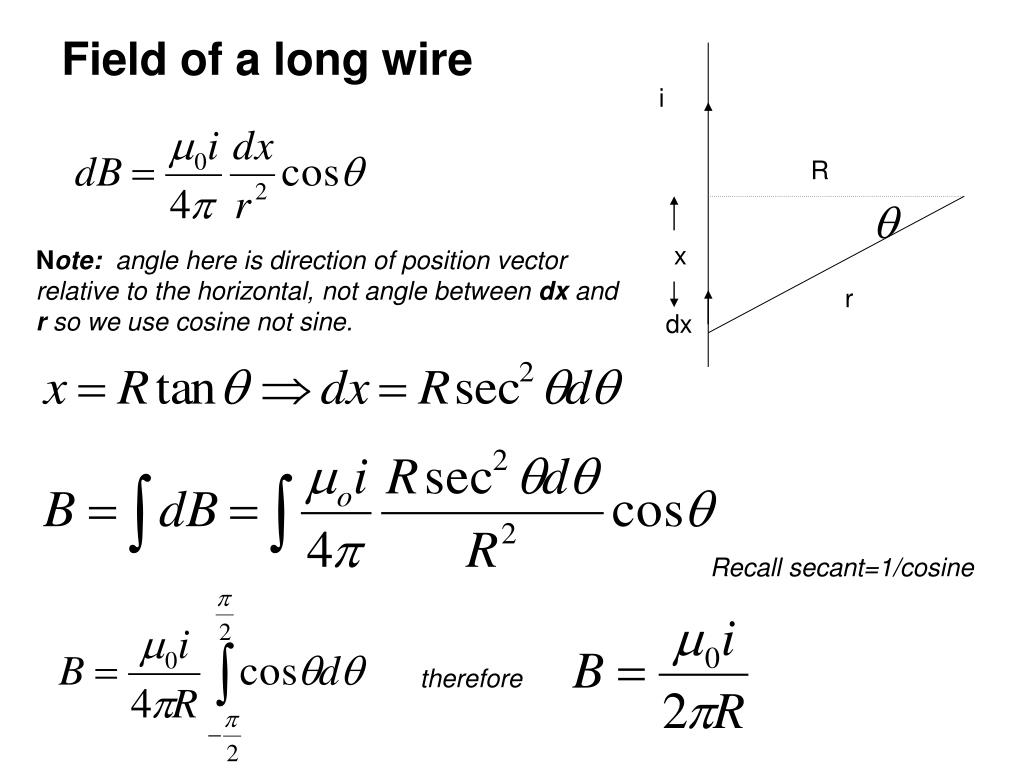
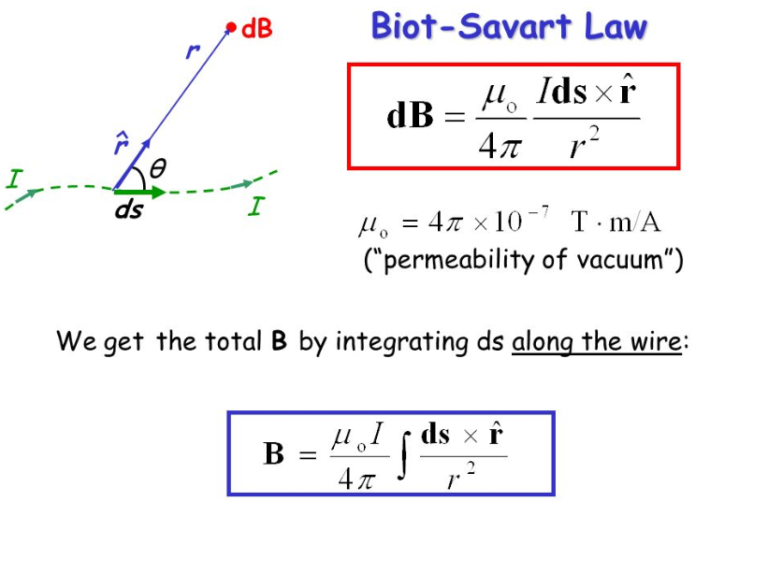
The Biot-Savart Law states that: → dB = μo 4πI→ dl × →r r3. The Biot-Savart Law represents a powerful straightforward method of calculating the magnetic field due to a current distribution. Calculate the magnetic field due to a long straight wire carrying a current I along the z axis in the positive z direction.


Biot savart law bapbasics

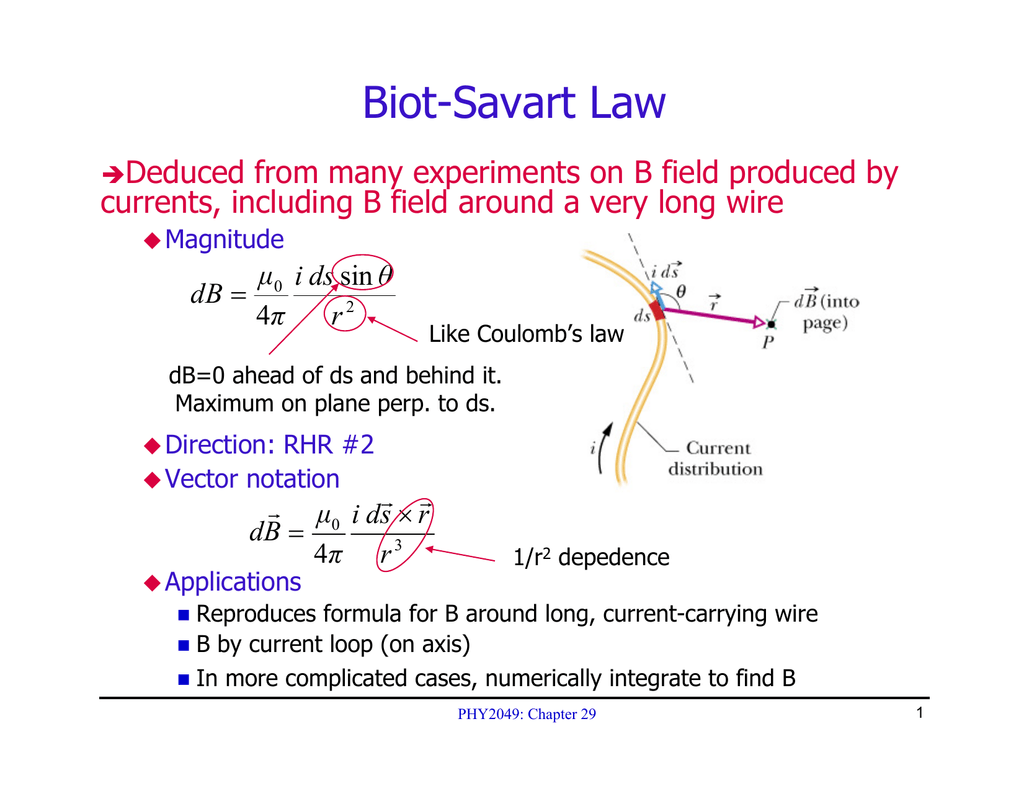
In any case, the Biot-Savart Law takes the form. δB = μ0 4π Iδs sin θ r2. (6.4.2) (6.4.2) δ B = μ 0 4 π I δ s sin θ r 2. The constant μ0 μ 0 is called the permeability of free space, "free space" meaning a vacuum. The subscript allows for the possibility that if we do an experiment in a medium other than a vacuum, the.


Biot savart law bapbasics

In physics, specifically electromagnetism, the Biot-Savart law ( / ˈbiːoʊ səˈvɑːr / or / ˈbjoʊ səˈvɑːr /) [1] is an equation describing the magnetic field generated by a constant electric current. It relates the magnetic field to the magnitude, direction, length, and proximity of the electric current. The Biot-Savart law is.


Biot savart law poleli

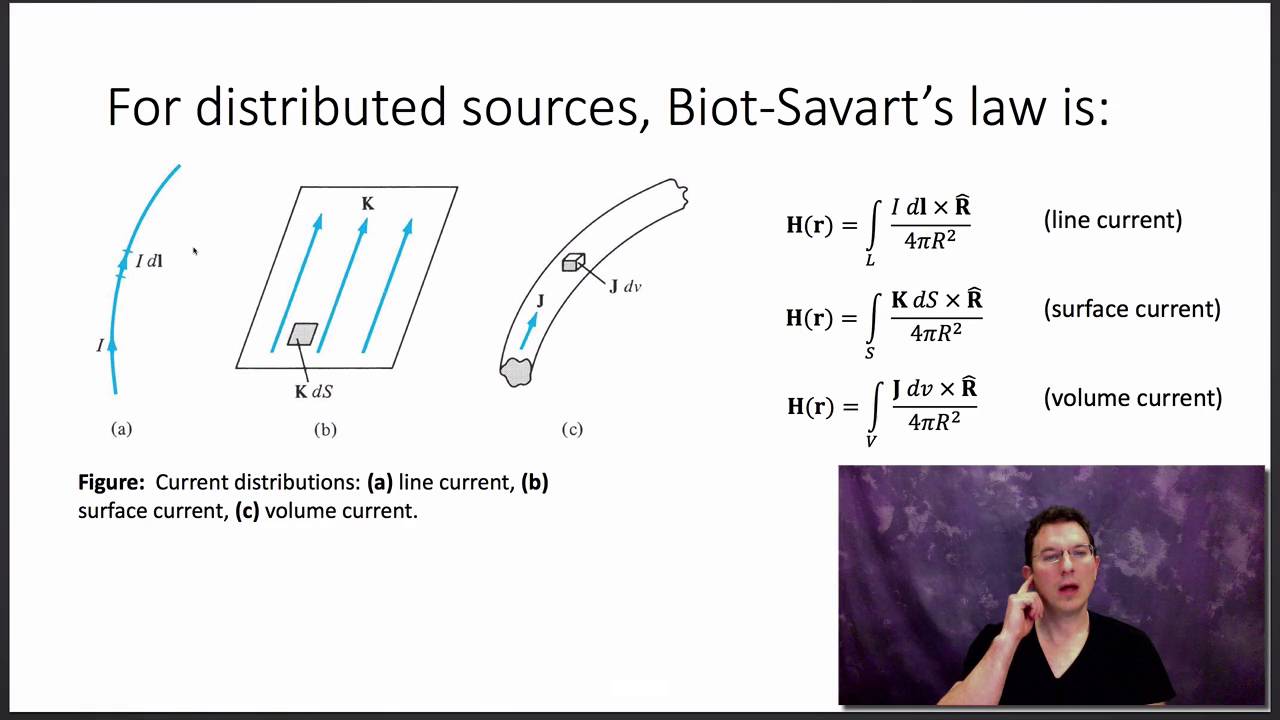
The Biot-Savart law (BSL) provides a method to calculate the magnetic field due to any distribution of steady (DC) current. In magnetostatics, the general solution to this problem employs Ampere's law; i.e., ∫CH ⋅ dl = Iencl. in integral form or. ∇ × H = J.


The BiotSavart Law Definition & Examples

The Biot-Savart law deflnes the magnetic fleld! B due a point charge q moving with a velocity!v as,! B = „0 4… (q!v £rb r2) (1) Here, rbis a unit vector that points from the position of the charge to the point at which the fleld is evaluated, r is the distance between the charge and the point at which the fleld is evaluated and „0.


Biot savart law ferdesigners

Biot-Savart Law gives the magnetic field produced due to a current carrying segment and its applications. Biot-Savart Law is an important law, since it can be used for very small conductors.


Applications of BiotSavart Law YouTube

The Biot-Savart law states that at any point ( Figure 9.1.1 ), the magnetic field due to an element of a current-carrying wire is given by. Figure 9.1.1 A current element produces a magnetic field at point P given by the Biot-Savart law. The constant is known as the permeability of free space and is exactly.


PPT Lecture 26 MON 27 OCT Fields Due to Currents BiotSavart Law PowerPoint

The Biot-Savart law allows us to determine the magnetic field at some position in space that is due to an electric current. More precisely, the Biot-Savart law allows us to calculate the infinitesimal magnetic field, \(d\vec B\), that is produced by a small section of wire, \(d\vec l\), carrying current, \(I\), such that \(d\vec l\) is co-linear with the wire and points in the direction of the.


What Is the Biot Savart Law? Example

The single moving point charge form of the Biot-Savart Law is B → = μ 0 4 π q v → × r ^ r 2. The permeability of free space, or the ease of producing a magnetic field in a vacuum, is a constant 4 π × 10 − 7 T ∗ m 2 C ∗ m s, denoted μ 0. The above equation describes the magnetic field vector B → at a point r ^ away from the.


BiotSavart Law of in Physics Class 12

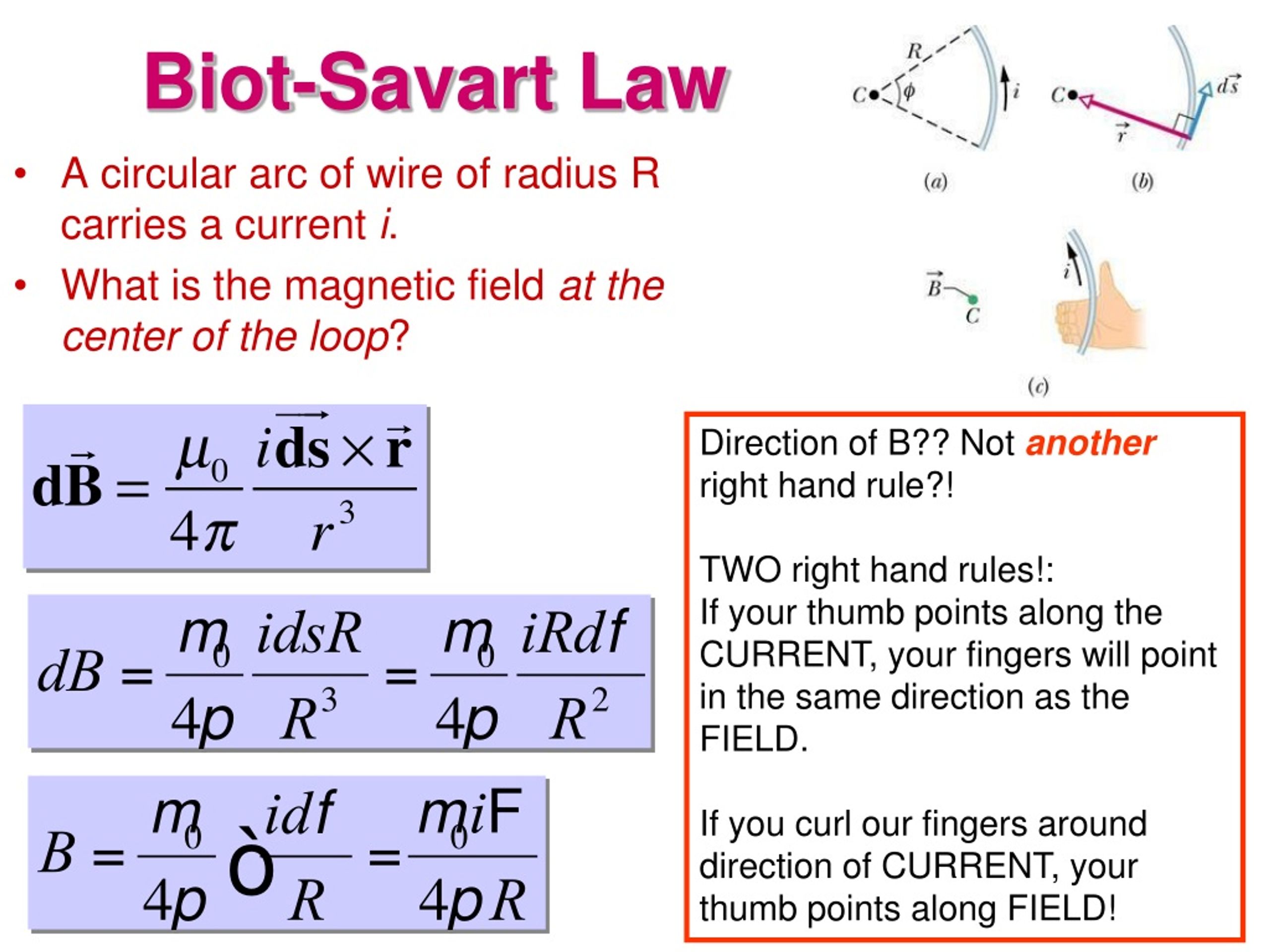
Transcript. Biot Savart law states that the magnetic field due to a tiny current element at any point is proportional to the length of the current element, the current, the sine of the angle between the current direction and the line joining the current element and the point, and inversely proportional to the square of the distance of that point.


BiotSavart Law

The Biot-Savart law is used for computing the resultant magnetic field B at position r generated by a steady current I (for example due to a wire): a continual flow of charges which is constant in time and the charge neither accumulates nor depletes at any point. The law is a physical example of a line integral, being evaluated over the path.


Biot Savart Law In Terms Of Current Density trueaload

Biot-Savart Law: Field of a "current element" ( analagous to a point charge in electrostatics). Ampère's Law: An integral theorem. Biot and Savart: each "current element" I ds (a very short length ds of wire, carrying current I) produces a field dB throughout space: dB. Ids. In reality, the current element is part of a complete.


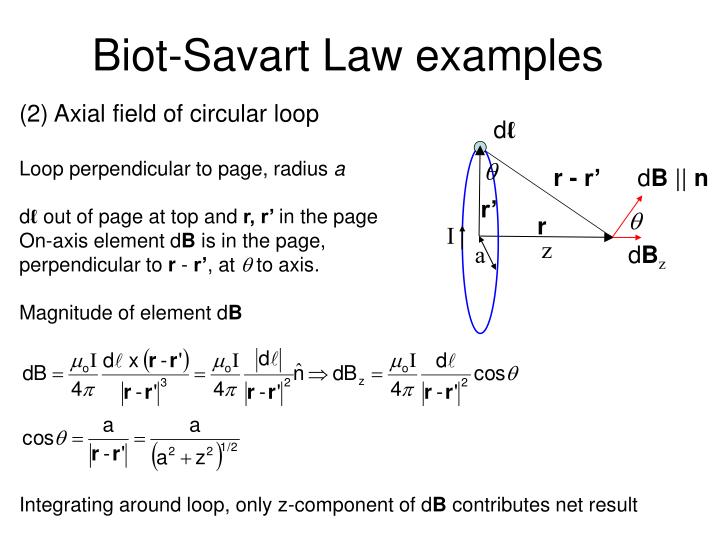
PPT BiotSavart Law PowerPoint Presentation ID4065417

saccharimetry. Biot-Savart law, in physics, a fundamental quantitative relationship between an electric current I and the magnetic field B it produces, based on the experiments in 1820 of the French scientists Jean-Baptiste Biot and Félix Savart. A current in a loop produces magnetic field lines B that form loops around the current.


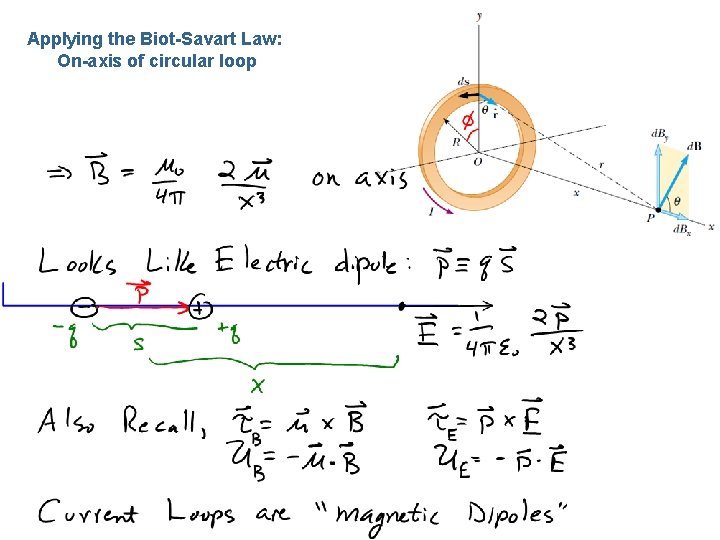
MIT visualizations Biot Savart Law Integrating a circular

To solve Biot-Savart law problems, the following steps are helpful: Identify that the Biot-Savart law is the chosen method to solve the given problem. If there is symmetry in the problem comparing B → B → and d l → , d l → , Ampère's law may be the preferred method to solve the question, which will be discussed in Ampère's Law .